Sau khi đã đi qua 3 bài viết về Delta, Gamma, Theta trong chủ đề Option Greeks, chúng ta sẽ cùng nhau tìm hiểu về cấu phần thứ 4, và cũng là thú vị nhất của Option Greeks, đó là Vega. Vega là đại lượng đo lường thay đổi của phí quyền chọn liên quan đến sự thay đổi trong biến động của tài sản cơ sở.
Vậy biến động tài sản cơ sở ở đây là gì? Đo lường biến động như thế nào? Chúng ta sẽ cùng tìm hiểu ngay sau đây.
Tính toán sự biến động
Như các bạn đã biết, để đo lường độ biến động nói chung, người ta sẽ sử dụng đại lượng Độ lệch chuẩn. Các bước cần để tính toán độ lệch chuẩn như sau:
- Tính toán giá trị trung bình
- Tính độ lệch = giá trị thực tế – giá trị trung bình)
- Tính Phương sai = bình Phương của tổng các độ lệch)
- Tính độ lệch chuẩn = căn bậc 2 của Phương sai
Sử dụng Excel để tính toán độ lệch chuẩn dựa trên dữ liệu là giá đóng cửa của tài sản.
Bước 1: Tải dữ liệu là giá đóng cửa của tài sản cơ sở
Bước 2: Tính toán lợi nhuận hàng ngày = Ln (Giá ngày hôm sau/Giá ngày hôm trước)
Bước 3: Sử dụng hàm STDEV để tính độ lệch chuẩn hàng ngày của lợi nhuận
Bước 4: Chuyển đổi mức độ biến động từ ngày sang mức độ biến động năm = (STDEV ngày) * (căn bậc 2 của thời gian)
Độ biến động và Phân phối chuẩn
Phân phối chuẩn là một kiến thức chúng ta đã được học ở Đại học

Biểu đồ Minh họa phân phối chuẩn
Nhắc lại về kiến thức về phân phối chuẩn và độ lệch chuẩn:
- Xác suất để quan sát được dữ liệu trong biên độ +/- 1 độ lệch chuẩn là 68%, 68% còn được gọi là độ tin cậy.
- Xác suất để quan sát được dữ liệu trong biên độ +/- 2 độ lệch chuẩn là 95%, 95% cò được gọi là độ tin cậy.
- Xác suất để quan sát được dữ liệu trong biên độ +/- 3 độ lệch chuẩn là 99.7%, 99.7% còn được gọi là độ tin cậy.

Đồ thị thể hiện phân phối chuẩn theo kiến thức chúng tôi đề cập ở phía trên.
Phân phối chuẩn và lợi nhuận cổ phiếu
Ở phần này chúng ta sẽ tìm hiểu mối quan hệ giữa lợi nhuận cổ phiếu và phân phối chuẩn.
Đây là biểu đồ phân phối lợi nhuận hàng ngày của NIFTY. Bạn có thể thấy rằng nó tuân theo phân phối chuẩn.
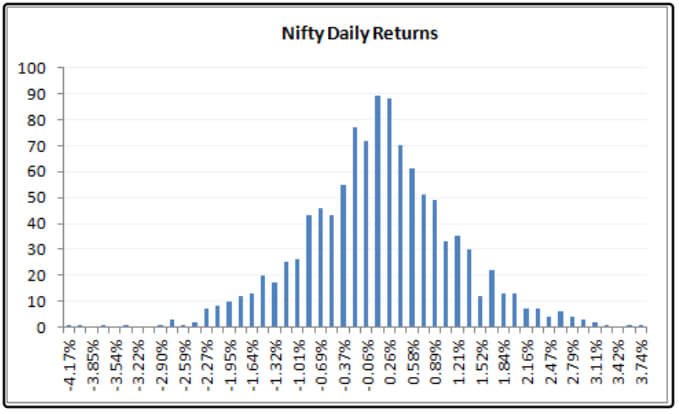
Giá trị lợi nhuận trung bình hàng ngày = 0,04%
Độ lệch chuẩn hàng ngày (Độ biến động) = 1,046%
Giá giao ngay NIFTY = 8337
Vậy giá NIFTY giao dich trong vòng 30 ngày tới hay 1 năm tới sẽ nằm trong phạm vi nào? Chúng ta sẽ sử dụng độ lệch chuẩn 1 và 2 với mức tin cậy 68% và 95%.
Trường hợp 1: Biên độ giao dịch của NIFTY trong 01 năm tới
Giá trị trung bình = 0,04%
Độ lệch chuẩn = 1,046%
Quy đổi đơn vị chuẩn theo năm, ta sẽ có:
Giá trị trung bình năm = 0,04%*252 = 10,08%. (Lưu ý: quy ước 1 năm có 252 ngày giao dịch)
Độ lệch chuẩn năm = 1,046%*Sqrt(252)=16,61%
- Với độ tin cậy 68% (1 độ lệch chuẩn), NIFTY trong vòng 1 năm tới sẽ giao dịch quanh ngưỡng
= 10,08% (+/-)16,61%
= -6,53% -> 26,69%
Từ đây ta tính được, trong vòng 1 năm tới giá sẽ giao dịch:
- Chặn trên = 8337 * e^(26,69%) = 10887
- Chặn dưới = 8337 * e^(-6,53%) = 7809
Kết luận, Trong vòng 1 năm tới xác suất 68% giá NIFTY sẽ giao dịch trong ngưỡng từ 7809 đến 10887.
- Với độ tin cậy 95% (2 độ lệch chuẩn), NIFTY trong vòng 1 năm tới sẽ giao dịch quanh ngưỡng
= 10,08 (+/-)2*16,61% = -23,14%->43,3%
Từ đây ta tính được, trong vòng 1 năm tới giá sẽ giao dịch:
- Chặn trên = 8337 * e^(43,3%) = 12854
- Chặn dưới = 8337 * e^(-23,14%) = 6614
Kết luận, trong vòng 1 năm tới xác suất 95% giá NIFTY sẽ giao dịch trong ngưỡng từ 6614 đến 12854.
Trường hợp 2: Biên độ giao dịch của NIFTY trong 30 ngày tới
Tính toán tương tự như trường hợp 1:
Giá trị trung bình quy 30 ngày = 0,04%*30 = 1,2%
Độ lệch chuẩn quỹ 30 ngày = 1,046%*Sqrt(30) = 5,73%
- Với độ tin cậy 68% (1 độ lệch chuẩn), NIFTY trong vòng 30 ngày tới sẽ giao dịch quanh ngưỡng
= 1,2% (+/-)5,75% = -4,53% -> 6,93%
Từ đây ta tính được, trong vòng 30 ngày tới giá sẽ giao dịch:
- Chặn trên = 8337 * e^(6,93%) = 8935
- Chặn dưới = 8337 * e^(-4,53%) = 7968
Kết luận, trong vòng 30 ngày tới, xác suất 68% giá NIFTy sẽ giao dịch trong ngưỡng từ 7968 đến 8935
- Với độ tin cậy 95% (2 độ lệch chuẩn), NIFTY trong vòng 30 ngày tới sẽ giao dịch quanh ngưỡng
= 1,2% (+/-)2*5,75% = -10,26% -> 12,66%
Từ đây ta tính được, trong vòng 30 ngày tới giá sẽ giao dịch:
- Chặn trên = 8337*e^(12,66%) = 9462
- Chặn dưới = 8337*e^(-10,26%) = 7524
Ứng dụng của độ biến động
Ở phần tiếp theo chúng ta sẽ nghiên cứu việc sử dụng Độ biến động để tính toán việc mua/ bán quyền chọn phù hợp cũng như đưa ra một điểm cắt lỗ chính xác. Sau khi đã dự tính được ngưỡng giá giao dịch trong 1 khoảng thời gian dự kiến, so sánh với giá thực hiện quyền chọn hiện tại, ta sẽ đưa ra được những quyết định đúng đắn hơn về việc có tham gia quyền chọn đó hay không.
Một Phương pháp hiệu quả để xác định điểm cắt lỗ khi bạn tham gia 1 giao dịch đó là sử dụng độ biến động của cổ phiếu. Hãy cùng nghiên cứu ví dụ sau để hiểu hơn nhé.

Ứng dụng của biến động
Bạn mua 1 cổ phiếu X giá 395, điểm cắt lỗ 385, giá mục tiêu là 417.
Ở đây lỗ = 395-385 = 10 điểm
Lãi mục tiêu = 417-395 = 32 điểm
Tỷ lệ Lãi/Lỗ = 32/10 = 3,2
Hãy đánh giá xem mức cắt lỗ 385 có phải là mức cắt lỗ hợp lý không?
- Bước 1: Tính mức độ biến độn hàng ngày của giá cổ phiếu X dựa trên data thị trường. Giả sử bạn tính được độ biến động hàng ngày bằng 1,8%.
- Dự kiến bạn nắm giữ vị thế trong 5 ngày, lúc này mức độ biến động 5 ngày sẽ = 1,8%*Sqrt(5) = 4,01%.
- Tính mức giá cắt lỗ dựa trên độ biến động 5 ngày = 395*(1 – 4,01%) = 379. Như vậy trong 5 ngày tới giá cổ phiếu X có thể giảm tới 379 điểm. Có nghĩa là bạn có thể sẽ chạm cắt lỗ, do đó bạn nên chọn điểm cắt lỗ thấp hơn 379, giả sử là 375, lúc này lỗ dự kiến nếu chạm cắt lỗ là 20 điểm.
Phân loại độ biến động

Phân loại độ biến động.
- Historical Volatility – Biến động lịch sử: sử dụng giá đóng cửa của tài sản cơ sở để tính toán độ biến động trong quá khứ.
- Forecasted Volatility – Dự báo biến động: dự báo sự biến động trong một khoảng thời gian xác định.
- Implied Volatility – Biến động hàm ý: thể hiện sự kỳ vọng của người tham gia thị trường về sự biến động
- Realized Volatility – Biến động thực tế: khi bạn muốn so sánh về Biến động hàm ý ngày hôm nay với Biến động hàm ý trong lịch sử.
Happy trading !