Tiến gần hơn đến mục tiêu xác định được rủi ro (phương sai) của danh mục đầu tư, trong bài viết này, chúng ta sẽ cùng tìm hiểu về hệ số tương quan và ma trận tương quan. Trong những nội dung trước, chúng ta đã biết được cách tính ma trận phương sai-hiệp phương sai, mặc dù chỉ một mình chúng thì sẽ không mang nhiều ý nghĩa. Tuy nhiên, đây chính là một trong những dữ kiện quan trọng sẽ được sử dụng trong bài viết này.

Hệ số tương quan là gì? Ý nghĩa của hệ số tương quan
Hệ số tương quan (Correlation) là giá trị thống kê đo lường mức độ mạnh yếu của mối quan hệ giữa hai biến số. Chúng có giá trị nằm trong đoạn từ -1 đến 1. Trong đó, hệ số tương quan mang giá trị âm cho thấy hai biến quan sát có mối quan hệ ngược chiều (nghịch biến hoàn toàn khi bằng -1), ngược lại, hai biến có tương quan dương khi hệ số tương quan có giá trị dương (đồng biến hoàn toàn khi bằng 1).
Như vậy, giá trị tuyệt đối của hệ số tương quan càng gần bằng 1 cho thấy mức độ tương quan giữa hai biến càng mạnh. Trong trường hợp chúng có giá trị bằng 0 thì hai biến quan sát độc lập hoàn toàn với nhau.
Hệ số tương quan được tính như thế nào?
Hệ số tương quan giữa hai biến bất kỳ được tính toán dựa trên công thức sau đây:
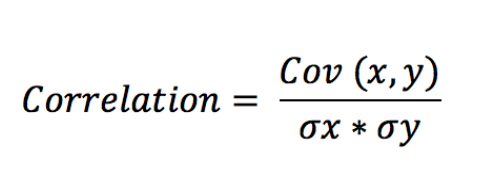
Trong đó:
Cov (x,y) là hiệp phương sai của hai biến x và y
σx là độ lệch chuẩn của x
σy là độ lệch chuẩn của y
Công thức trên hoàn toàn dễ dàng áp dụng trong trường hợp có hai cổ phiếu. Vậy đối với một danh mục 5 cổ phiếu thì hệ số tương quan được xác định như thế nào? Lúc này, chúng ta cần vận dụng các phép toán với ma trận.
Khi đó, hệ số tương quan của danh mục sẽ được biểu diễn dưới dạng ma trận hệ số tương quan giữa các cổ phiếu với nhau, có kích thước nxn. Như vậy với một danh mục 5 cổ phiếu đã xuất hiện trong ví dụ ở chương trước, chúng ta cần một ma trận với kích thước 5×5.
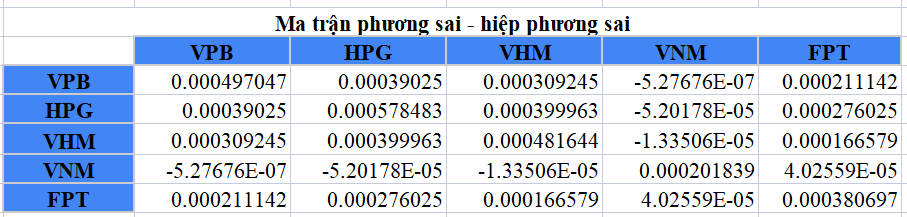
Cũng với ví dụ về 5 cổ phiếu bao gồm: VPB, HPG, VHM, VNM và FPT, ta có ma trận phương sai – hiệp phương sai như sau:
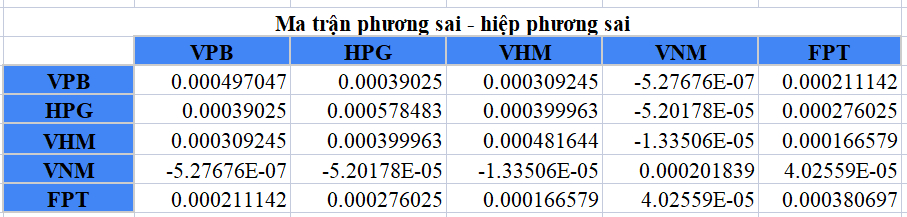
Dựa vào công thức cùng với các hệ số tương quan đã tính được trong ma trận phía trên, đến đây chúng ta cần tính được mẫu số là tích độ lệch chuẩn của tất cả các cổ phiếu có trong danh mục.
Để làm được điều này, trước hết chúng ta cần tính được độ lệch chuẩn của riêng từng cổ phiếu. Việc tính toán tương đối đơn giản khi căn bậc hai của phương sai chính bằng độ lệch chuẩn. Bạn chỉ cần sử dụng hàm “STDEV()” trong excel đối với dãy lợi suất hàng ngày của cổ phiếu, kết quả sẽ ra độ lệch chuẩn lợi suất của cổ phiếu đó.

Bước trên mới tính được độ lệch chuẩn của riêng từng cổ phiếu, việc chúng ta cần làm bây giờ chính là tính được độ lệch chuẩn của các cặp cổ phiếu trong danh mục. Cách làm phổ biến nhất chính là lập ma trận bằng cách nhân độ lệch chuẩn của từng cổ phiếu với dãy độ lệch chuẩn bị nghịch đảo so với hình trên. Cụ thể như sau:
Đầu tiên, lập ma trận có kích thước 5×5 như sau:

Tiêp theo đó, nhân dãy giá trị độ lệch chuẩn đã tính được trước đó với dãy chuyển bị của chính nó (đảo ngược lại vị trí từ đầu xuống cuối và ngược lại). Hình minh họa dưới đây sẽ làm rõ bước làm này:

Hãy luôn lưu ý sử dụng tổ hợp phím ‘ctrl+shift+enter’ đối với những phép toán liên quan đến ma trận hoặc dãy dữ liệu trong excel.

(1)
Nhìn lại công thức tính hệ số tương quan:
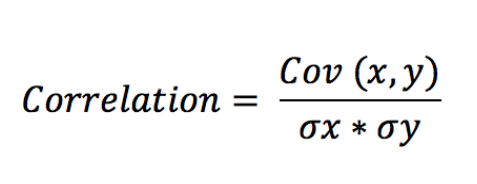
Có thể thấy, tử số chính là ma trận phương sai-hiệp phương sai của danh mục (kết quả chúng ta đã tính được trong chương trước) và mẫu số là ma trận độ lệch chuẩn mới có được ở phía trên.
(2)
Như vậy, để ra được ma trận hệ số tương quan, chúng ta chỉ cần thực hiện phép chia ma trận (2) với ma trận (1).

Ma trận hệ số tương quan sẽ có kết quả như sau:

Ma trận trên cho chúng ta thấy hệ số tương quan giữa các cặp cổ phiếu với nhau. Ví dụ, cổ phiếu HPG và VPB có giá trị tương quan bằng 0.65117. Giá trị này không thay đổi khi ta xem xét cặp VPB và HPG. Chính vì vậy có thể thấy, ma trận biểu thị các giá trị đối xứng nhau thông qua đường chéo.
Thông thường, giá trị tương quan giữa một biến và chính nó được biểu thị bằng đường chéo của ma trận luôn có giá trị bằng 1. Tuy nhiên trong ví dụ này, do dữ liệu tính toán trong khoảng thời gian tương đối ngắn (số ngày giao dịch thực tế trong 1 tháng), chính vì vậy mà giá trị tương quan chỉ đạt ở mức cao mà chưa thể đạt giá trị max bằng 1.
Phương sai của danh mục đầu tư
Sau khi đã tính toán được ma trận hệ số tương quan của danh mục cổ phiếu ở phần trước, trong phần này, chúng ta sẽ tiến hành phân tích mức độ rủi ro của danh mục dựa trên việc tính phương sai của nó.
Đầu tiên, cần xác định được tỷ trọng của từng cổ phiếu trong danh mục đầu tư. Đây là giá trị biểu thị cho việc bạn bỏ bao nhiêu tiền để mua từng mã trong danh mục gồm 5 cổ phiếu kể trên. Giả sử với $1000 vốn khả dụng, tôi quyết định phân bổ vào danh mục như sau:
- VPB $100 (10%)
- HPG $200 (20%)
- VHM $400 (40%)
- VNM $200 (20%)
- FPT $100 (10%)
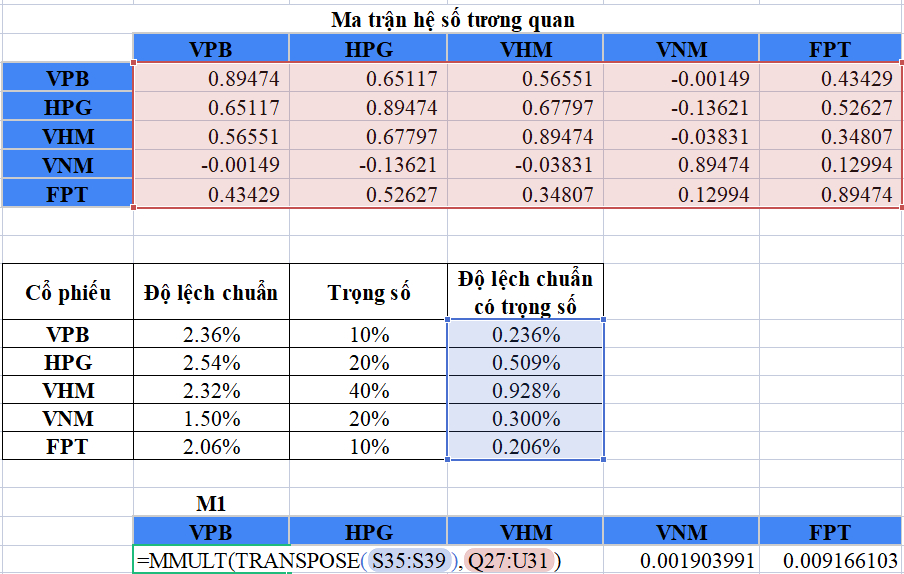
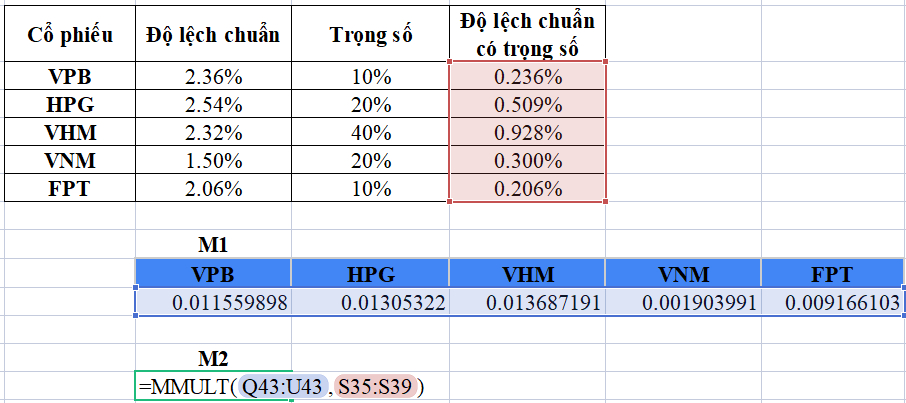
Bước tiếp theo là tính toán độ lệch chuẩn có trọng số. Độ lệch chuẩn có trọng số chỉ đơn giản là tỷ trọng của một cổ phiếu nhân với độ lệch chuẩn tương ứng của nó. Ví dụ: độ lệch chuẩn của VPB là 2,36%, khi đó độ lệch chuẩn có trọng số của nó sẽ là 10% * 2,36% = 0,236%
Kết quả tính toán cụ thể như sau:

*Lưu ý: Tổng tỷ trọng của các cổ phiếu trong một danh mục phải bằng 100%
Đến đây, chúng ta đã có đủ dữ kiện để tính toán “Phương sai của danh mục đầu tư”. Công thức cụ thể như sau:
Phương sai của danh mục = Căn bậc hai (ma trận chuyển vị của độ lệch chuẩn có trọng số * ma trận hệ số tương quan * dãy độ lệch chuẩn có trọng số)
Thông qua 3 bước cụ thể như sau:
Bước 1. Thực hiện phép nhân ma trận giữa dãy độ lệch chuẩn có trọng số với ma trận hệ số tương quan rồi thực hiện phép chuyển vị để ra một ma trận có 5 cột. Gọi ma trận này là M1, ta có phép tính và kết quả như sau:
Bước 2. Nhân ma trận vừa tìm được với dãy độ lệch chuẩn có trọng số, kết quả là một số cụ thể gọi là M2:
Bước 3. Căn bậc hai số vừa tìm được để ra giá trị phương sai của danh mục

Kết quả của phép toán trên là 1,57%, là phương sai danh mục đầu tư của danh mục 5 cổ phiếu chúng ta cần tìm.
Như vậy đến đây, chúng ta đã tìm được giá trị cuối cùng cần tính toán trong chuỗi bài viết. Trong bài viết tiếp theo, chúng tôi sẽ giải thích rõ ràng hơn về ý nghĩa của con số này.
Happy Trading !