Khi quản lý một danh mục đầu tư, điều mà chúng ta thường quan tâm đó chính là tỷ suất sinh lời toàn danh mục này ra sao. Thay vì nhìn vào những con số, có một cách để trực quan hóa tỷ suất sinh lời danh mục dưới dạng hình ảnh giúp những nhà đầu tư dễ dàng theo dõi hơn đó chính là sử dụng đường cong vốn chủ sở hữu.
Tỷ suất lợi nhuận là gì?
Tính toán tỷ suất sinh lời toàn danh mục đầu tư là giá trị trung bình có trọng số của tỷ suất sinh lợi kỳ vọng cho từng yếu tố cấu thành nên danh mục đó. Và trọng số của các yếu tố cấu thành được tính theo tỷ lệ phần trăm trên tổng giá trị danh mục.

Đường cong vốn chủ sở hữu (Equity Curve) là gì?
Đường cong vốn chủ sở hữu hay equity curve là đường biểu diễn tỷ suất sinh lời của danh mục đầu tư trên thang điểm 100. Một cách đơn giản hơn, nó cho chúng ta biết được rằng với $100 đầu tư ban đầu, danh mục sẽ đạt tỷ suất sinh lời ra sao trong suốt chu kỳ quan sát. Từ thước đo này, chúng ta cũng có thể dễ dàng so sánh với những chỉ số nổi bật trên thị trường như VNIndex hay VN30…v.v…
Trong bài viết này, chúng ta sẽ xây dựng đường cong vốn chủ sở hữu cho danh mục gồm 5 cổ phiếu trong những ví dụ trước đó để quan sát hiệu quả hoạt động của nó ra sao trong khoảng thời gian 1 tháng
Dưới đây là danh mục của chúng ta với tỷ trọng mỗi mã cổ phiếu tương ứng:
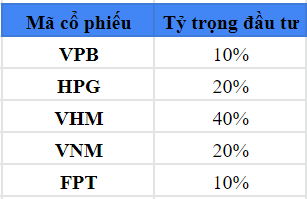
Lưu ý, tỷ trọng đầu tư hay “investment weight” chính là tỷ lệ tiền bạn phân bổ cho từng mã cổ phiếu trên tổng vốn đầu tư khả dụng của mình. Trong ví dụ được sử dụng ở bài biết này, với tổng vốn đầu tư 10 triệu đồng, chúng ta đã dành 1 triệu cho VPB, tương ứng với tỷ trọng 10% trong danh mục.

Bên cạnh cột lợi suất là cột tỷ trọng đầu tư tương ứng của mỗi cổ phiếu. Ở phía cuối hàng ngang, chúng ta có cột giá trị ban đầu của danh mục (10 triệu đồng) cùng tổng tỷ trọng 100%. Lưu ý, tổng tỷ trọng của 5 cổ phiếu đơn lẻ trong danh mục phải luôn luôn bằng 100%.
Bây giờ, hãy đi vào chi tiết từng cổ phiếu đơn lẻ, bắt đầu với VPB. Với tỷ trọng 10%, tổng mức đầu tư ban đầu cho VPB là 1 triệu đồng. Dựa trên mức độ biến động của giá đóng cửa của ngày 5/1 so với ngày 4/1, chúng ta tính được lợi suất theo ngày, sau đó nhân với 1 triệu. Như vậy khoản đầu tư 1 triệu vào VPB sau hôm 4/1 sẽ là ~985K. Đó cũng sẽ là mức giá bắt đầu để so sánh với giá của ngày 5/1.

Vào ngày 4/1, chúng ta quyết định mua VPB với mức giá là 36.05K. Trên thực tế về mặt giao dịch, sẽ không dễ để chúng ta muốn mua cổ phiếu ở một mức giá nào đó là sẽ mua được ngay và cổ phiếu sẽ về ngay tài khoản (quy tắc T+2).
Tuy nhiên ở ví dụ này, chúng ta giả định việc giao dịch sẽ được thực hiện thành công ngay sau khi quyết định. Như vậy vào ngày 4/1, chúng ta đã dùng 10% số tiền mình có, tức 1 triệu đồng để mua VPB ở mức giá 36.05K. Vào ngày tiếp theo, VPB đóng cửa ở giá 35.5K giảm 1.53% so với hôm trước. Điều này cũng có nghĩa là 1 triệu đã bị giảm đi 1.53% còn ~985K.
Tương tự, đến ngày tiếp theo, giá đóng cửa của VPB là 35.15K, như vậy khoản đầu tư đã giảm 0.99% xuống ~990K. Những ngày tiếp theo, đối với sự tăng giảm của giá cổ phiếu, chúng ta cũng sẽ hiểu theo như logic như vậy.
Hình dưới đây sẽ minh họa cho những giải thích ở trên:

*Cột màu xanh cho thấy sự biến động hàng ngày của khoản tiền đã được phân bổ vào các cổ phiếu.
Câu hỏi đặt ra ở đây là, ban đầu chúng ta phân bổ 10 triệu đồng vào 5 cổ phiếu với 5 mức tỷ trọng khác nhau. Nhưng khi giá cổ phiếu biến động hàng ngày, liệu tổng tất cả các mức giá sau khi tính theo tỷ trọng đầu tư rồi có còn là 10 triệu nữa hay không?
Trả lời được câu hỏi này sẽ giúp chúng ta thấy được cách danh mục biến động là như thế nào.

Tương tự như dòng thứ 2, việc lần lượt tính được giá trị tổng giá trị hàng ngày sẽ cho chúng ta một chuỗi giá trị theo thời gian mức độ biến động của danh mục đầu tư.

Từ chuỗi dữ liệu theo thời gian đó, chúng ta hoàn toàn có thể biểu diễn được đường cong vốn chủ sở hữu (Equity Curve hay EQ Curve) bằng biểu đồ đường nối các điểm dữ liệu trên. Cụ thể hình ảnh minh họa của nó như sau:
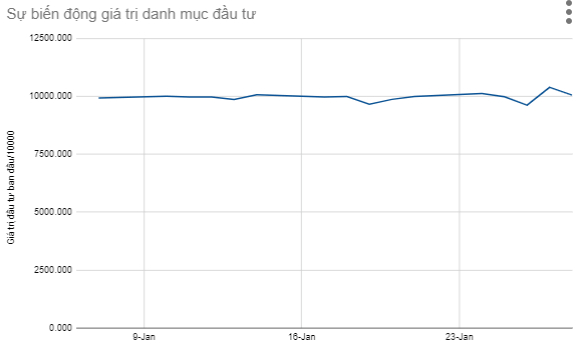
Rất đơn giản và trực quan đúng không nào? Đường cong vốn chủ sở hữu là một cách rất phổ biến để biểu diễn hiệu quả của danh mục đầu tư. Nó đưa ra một ước tính nhanh chóng về lợi nhuận do danh mục đầu tư tạo ra. Trong trường hợp này, chúng ta bắt đầu với khoản đầu tư là 10 triệu đồng và sau 1 tháng, danh mục đầu tư được định giá là 10,043,564 đồng. Cụ thể như sau:

Vì vậy, không cần suy nghĩ nhiều, chúng ta biết danh mục đầu tư đã đạt gần 0.43% trong khoảng thời gian 1 tháng quan sát, hay đó cũng chính là lợi suất của danh mục trong một tháng qua.
Một cách tiếp cận khác về rủi ro của danh mục đầu tư
Trong những bài viết trước, chúng ta đã biết cách tính phương sai của một danh mục đầu tư thông qua việc tính độ lệch chuẩn của từng cổ phiếu. Chúng ta cũng đã biết độ lệch chuẩn chính là đại diện cho mức độ biến động (volatility) của cổ phiếu, một khái niệm đại diện cho mức độ rủi ro của cổ phiếu.
Để tính được độ lệch chuẩn, chúng ta đã sử dụng hàm ‘=STDEV()’ trong Excel đối với lợi suất hàng ngày của cổ phiếu.
Trong khi đó, ở bài viết này, chúng ta có giá trị hàng ngày của danh mục, biến động xung quanh mốc $1000 bỏ ra ban đầu. Thử hình dung một danh mục hiện giờ cũng giống như một cổ phiếu, vậy việc tính lợi suất hàng ngày của nó cũng giống như việc chúng ta tính lợi suất hàng ngày của các cổ phiếu vậy.
Bên cạnh đó, việc chúng ta sử dụng hàm ‘=STDEV()’ đối với các mốc lợi suất của danh mục này có phải chính là việc chúng ta đi tính độ lệch chuẩn hay nói cách khác chính là rủi ro/phương sai của toàn danh mục hay không. Bạn đã hình dung ra sự liên quan ở đây chưa?
Chính xác là chúng ta đang tính phương sai của danh mục đầu tư theo một hướng tiếp cận hoàn toàn mới!!!
Trong bài viết trước, giá trị phương sai của danh mục đầu tư mà chúng ta đã tính được là:
1,57%
Trước đó chúng ta đã tính ra giá trị này dựa trên việc sử dụng phép nhân ma trận và phương pháp ma trận hệ số tương quan.
Trong bài viết này, chúng ta coi 1 danh mục giống như một cổ phiếu và tính lợi suất hàng ngày của nó. Sau đó, tính độ lệch chuẩn của danh mục dựa trên chuỗi lợi suất vừa tìm được. Kết quả cuối cùng sẽ tương tự như kết quả chúng ta đã tìm được ở phía trên.
Dưới đây là lợi suất hàng ngày của danh mục đầu tư:

Sau khi có được chuỗi lợi suất hàng ngày, chúng ta sẽ sử dụng hàm ‘=STDEV()’ để tính độ lệch chuẩn của danh mục.
Như bạn có thể thấy, kết quả vừa tìm được tương tự với giá trị chúng ta đã tính được ở bài viết trước.
Happy Trading !