Nhắc lại phần trước
Trong bài viết trước, chúng ta đã tìm hiểu về khái niệm phương sai (variance) và hiệp phương sai (covariance) gắn với hai loại rủi ro thường thấy là rủi ro hệ thống và rủi ro phi hệ thống. Sau khi hiểu được sự khác biệt cơ bản giữa 2 loại rủi ro này, chúng ta sẽ tiếp cận với rủi ro của danh mục đầu tư hay còn được gọi là phương sai của danh mục.
Cụ thể, phương sai (variance) là mức độ chênh lệch giữa lợi suất của một cổ phiếu so với lợi tức trung bình của chính nó. Hiệp phương sai (covariance) là phương sai của lợi tức cổ phiếu này so với lợi tức của một cổ phiếu khác.
Trong các ví dụ đã được sử dụng, các công thức chỉ mới được áp dụng cho một nhóm gồm 2 cổ phiếu, trong khi trên thực tế một danh mục lại bao gồm nhiều hơn thế. Chính vì vậy, để ước tính phương sai, hiệp phương sai và giá trị tương quan của danh mục đầu tư, chúng ta cần sử dụng ma trận phương sai – hiệp phương sai.
Trong chương này, chúng ta sẽ cùng thảo luận về cách ước tính ‘phương sai – hiệp phương sai’ của một danh mục đầu tư; thông qua phép nhân ma trận và một số khái niệm liên quan. Kết quả ma trận ‘hiệp phương sai’ đóng vai trò quan trọng trong việc tính toán ma trận hệ số tương quan. Đây chính là cơ sở để tính toán phương sai của danh mục đầu tư, từ đó xác định được mức độ rủi ro khi nắm giữ một danh mục cổ phiếu là như thế nào.
Trong khi thảo luận, chúng ta cũng sẽ đề cập đến “phân bổ tài sản” và cách nó tác động đến lợi nhuận và rủi ro của danh mục đầu tư. Đồng thời, bạn cũng sẽ cần phải tiếp cận nhanh với khái niệm “giá trị có rủi ro” hay VaR (Value at Risk).
Xem xét chi tiết rủi ro từ góc độ của một trader, nội dung chương này sẽ giúp bạn xác định được rủi ro giao dịch và các cách để giảm thiểu chúng.
Ma trận Phương sai – Hiệp phương sai (Variance – Covariance Matrix)
Trước khi tiếp tục, chúng ta cần làm rõ cụm từ ‘ma trận Phương sai – Hiệp phương sai’. Ở đây nó mang nghĩa là một ma trận gồm cả 2 giá trị phương sai và hiệp phương sai hay là 2 ma trận phương sai và ma trận hiệp phương sai riêng biệt?
Câu trả lời đó là: Một ma trận duy nhất gồm các giá trị phương sai và hiệp phương sai. Giả dụ nếu có 5 cổ phiếu, thì ma trận này thể hiện giá trị phương sai của một cổ phiếu và hiệp phương sai của nó với 4 cổ phiếu còn lại. Ví dụ sau đây sẽ giúp chung ta dễ dàng hình dung hơn. Bên cạnh đó, bạn cũng cần biết một số phép toán cơ bản với ma trận. Nếu chưa biết thì video dưới đây của Khan Academy sẽ giúp bạn hiểu rõ hơn về phép nhân ma trận tại đây.
Một danh mục đầu tư đa dạng (có tính thuyết phục cao) thường bao gồm khoảng 10-15 cổ phiếu. Tuy nhiên, việc sử dụng ma trận với kích thước này để trực quan hóa trên excel sẽ rất phức tạp và với nhiều người mới bắt đầu có thể sẽ cảm thấy choáng ngợp với kích thước của ma trận. Chính vì vậy, tôi quyết định sẽ sử dụng một danh mục đầu tư gồm 5 cổ phiếu để việc tính toán vừa đảm bảo tính trực quan, vừa không gây khó khăn với người mới bắt đầu.
Giả sử, 5 cổ phiếu trong danh mục đầu tư của tôi bao gồm: VPB, HPG, VHM, VNM và FPT
Kích thước của ma trận hiệp phương sai cho danh mục đầu tư gồm 5 cổ phiếu sẽ là 5 x 5. Một cách tổng quát, nếu có ‘k’ cổ phiếu trong danh mục, thì kích thước của ma trận hiệp phương sai sẽ là kxk (gồm k hàng, k cột).
Công thức để xác định ma trận hiệp phương sai như sau:
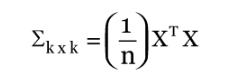
Trong đó:
k là số lượng cổ phiếu trong danh mục đầu tư
n là số quan sát
X là ma trận lợi nhuận thặng dư có kích thước nxk, sẽ được trình bày rõ ràng ngay sau đây
XT = ma trận chuyển vị của ma trận X
Cụ thể, chúng ta cần tính được ma trận lợi nhuận thặng dư có kích thước n x k trước; sau đó nhân ma trận này với ma trận chuyển vị của nó. Đây là một phép nhân ma trận với kết quả sẽ là một ma trận có kích thước k x k. Sau đó chúng ta chia mỗi phần tử của ma trận k x k này cho n quan sát. Kết quả nhận được là ma trận hiệp phương sai k x k.
Để trực quan hóa, tôi sẽ sử dụng MS Excel áp dụng công thức tính ma trận cho danh mục gồm 5 cổ phiếu được đề cập ở trên. Dữ liệu nghiên cứu bao gồm giá đóng cửa hàng ngày của 5 cổ phiếu trên trong 1 tháng qua.
Bước 1 – Tính lợi suất hàng ngày của cổ phiếu.
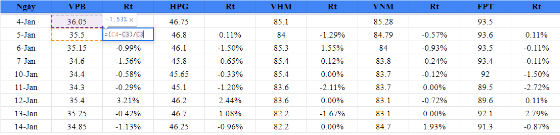
Trong hình trên, bạn có thể dễ dàng nhìn thấy lợi suất hàng ngày của từng cổ phiếu được tính ở ngay bên cạnh các cột giá đóng cửa.
Bước 2 – Tính giá trị trung bình của lợi suất hàng ngày đối với mỗi cổ phiếu bằng cách sử dụng hàm ‘AVERAGE’.

Bước 3 – Tính ma trận lợi nhuận thặng dư
Ma trận lợi nhuận thặng dư được định nghĩa là sự khác biệt giữa lợi nhuận hàng ngày của cổ phiếu so với lợi nhuận trung bình của nó. Nếu bạn còn nhớ thì chúng ta đã làm điều này trong chương trước khi thảo luận về hiệp phương sai giữa hai cổ phiếu.
Ma trận lợi nhuận thặng dư được tính theo cách sau:

Cần lưu ý, ma trận kết quả có kích thước n x k, trong đó n đại diện cho số lượng quan sát (trong ví dụ này là 19) và k là số lượng cổ phiếu (5). Vì vậy, trong ví dụ của chúng tôi, kích thước ma trận là 19 x 5, kí hiệu là ma trận X.
Bước 4 – Thực hiện phép nhân ma trận XT với X để tạo một ma trận có kích thước kxk
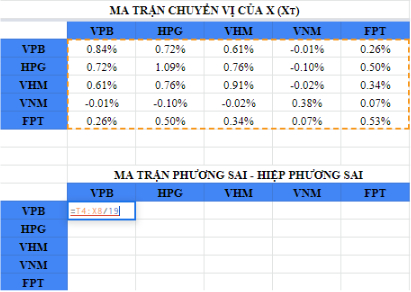
XT là ma tận chuyển vị của X, được tạp ra bằng cách hoán đổi các hàng và cột của ma trận ban đầu X. Lưu ý, ma trận kết quả từ phép toán này sẽ tạo ra ma trận k x k, trong đó k biểu thị số lượng cổ phiếu trong danh mục đầu tư. Trong trường hợp của chúng ta, kích thước ma trận sẽ là 5 x 5.
Liệt kê các cổ phiếu theo hàng và cột như sau:
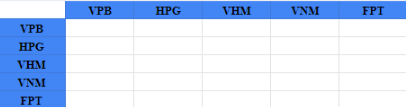
Sử dụng hàm = ‘MMULT ((transpose X), X), trong đó X là ma trận lợi nhuận thặng dư

Lưu ý rằng, trong khi áp dụng hàm này, bạn cần đảm bảo rằng bạn đánh dấu ma trận k x k. Lưu ý là sau khi nhập xong công thức, bạn không thể nhấn ‘enter’ trực tiếp mà thay vào đó, hãy nhấn ctrl + shift + enter.
Bước 5 – Đến đây, hãy chia mỗi phần tử của ma trận XT X vừa tìm được cho tổng số quan sát n. Xem lại công thức sau để rõ hơn:
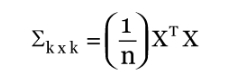
Thay vì phải chia từng ô cho 19, hãy chọn toàn bộ mảng chứa ma trận XTX, chia cho 19 rồi nhấn tổ hợp phím ctrl + shift + enter (do đây là một hàm tính chứ không phải phép tính thông thường).
Kết quả trả về sẽ là ma trận hiệp phương sai cần tìm:

Từ bảng kết quả trên, tại ô đã được đánh dấu đỏ có thể thấy, hiệp phương sai của HPG với VHM cũng chính bằng hiệp phương sai giữa VHM và HPG, không có sự khác biệt ở đây (đều bằng 0.04%).
Bên cạnh đó, nhìn vào ô xanh bạn có thể thấy hiệp phương sai của VPB với chính nó bằng 0.04%. Giá trị này nói lên điều gì? Không gì khác, giá trị hiệp phương sai giữa một cổ phiếu với chính nó chính bằng giá trị phương sai.
Đó chính là lý do vì sao mà ma trận này được gọi là ma trận Phương sai-Hiệp phương sai bởi nó chứa cả hai giá trị trên.
Đến đây, bạn đã biết cách tính được ma trận phương sai-hiệp phương sai rồi. Tuy nhiên, chỉ mỗi ma trận này không nói lên điều gì cả. Cái chúng ta thật sự cần là “Ma trận Hệ số tương quan” – nội dung quan trọng và là đích đến để chúng ta ước tính được phương sai/rủi ro của danh mục đầu tư. Hãy cùng thảo luận trong chương tiếp theo!
Bạn có thể sử dụng dữ liệu nghiên cứu tại đây.
Happy Trading !