Trong đầu tư, một tâm lý thông thường của nhà đầu tư là dự đoán trước khoản lợi nhuận và kỳ vọng nó sẽ là con số lớn nhất mà chúng ta có thể nhận được trong tương lai. Tuy nhiên, nếu có một cái nhìn khách quan hơn, chúng ta đều phải thừa nhận rằng rủi ro đôi khi có thể đến rất bất ngờ và khiến chúng ta khó có thể trở tay kịp.
Chính vì vậy, các nhà đầu tư thường tìm tới các biện pháp phòng ngừa rủi ro để giảm thiểu thấp nhất thiệt hại có thể có. Và để tiến hành được các biện pháp này, việc ước lượng được mức thiệt hại lớn nhất mà chúng ta có nguy cơ phải chịu đóng vai trò vô cùng quan trọng. Trong khuôn khổ bài viết này, chúng ta sẽ tiếp cận với phương pháp quản trị rủi ro dựa trên một loại khái niệm vô cùng quan trọng, đó là Giá trị chịu rủi ro – Value at Risk. Trước hết:
Giá trị chịu rủi ro – Value at Risk là gì?
Chúng ta đã từng nghe nhiều tới thuật ngữ “Thiên nga đen”, được phổ biến bởi Nassim Nicholas Taleb, đề cập tới những sự kiện cực kỳ hiếm khi xảy ra nhưng để lại hậu quả vô cùng nghiêm trọng trong lịch sử. Vì tính chất hiếm khi xảy ra, những sự kiện Thiên nga đen vượt qua mọi dự đoán bình thường.
Tại sao lại là Thiên nga đen và nó liên quan gì tới VaR?
Trong lịch sử kinh tế thế giới, chúng ta đã trải qua nhiều sự kiện “Thiên nga đen” mà hậu quả sau đó thật sự thảm khốc. Có thể kể đến Bong bóng Dotcom (Dotcom Bubble) xảy ra vào năm 2001 khi mà sự kỳ vọng quá lớn của nhà đầu tư vào những công ty dotcom (những công ty sử dụng Internet làm nền tảng chính cho hoạt động kinh doanh của mình) dẫn đến việc chúng được định giá quá cao trong khi thực tế các công ty này sở hữu rất ít tài sản vật chất và có lịch sử lợi nhuận không rõ ràng.
Và khi các công ty này công bố lợi nhuận thực tế bị thiếu hụt, các nhà đầu tư đã nhanh chóng tìm tới các công cụ đầu tư khác, dẫn tới tình trạng bán tháo cổ phiếu khiến giá bị sụt giảm một cách nhanh chóng và sự sụp đổ của nhiều công ty bắt đầu diễn ra gây hậu quả nghiêm trọng với nền kinh tế.
Ngoài Dotcom Bubble, một sự kiện Thiên nga đen có lẽ còn tồi tệ hơn nữa là Bong bóng địa ốc (2008) khởi nguồn tại Hoa Kỳ khiến cho thị trường nhà đất của quốc gia này sụp đổ sau đó đã lan rộng ra toàn cầu và để lại hậu quả vô cùng nặng nề.
Cũng ngay trong năm đó, Zimbabwe đã rơi vào tình trạng siêu lạm phát (hiện tượng lạm phát nghiêm trọng nhất) khi mà lạm phát của quốc gia này “nhảy số” từng giờ. Đỉnh điểm, lạm phát của Zimbabwe có khi đã lên tới 500 tỷ %, tờ tiền có mệnh giá cao nhất lên tới 100 nghìn tỷ USD cũng chỉ để hạn chế tình trạng người dân nước này phải chở cả xe tiền đi mua đồ dùng thiết yếu.

Tình trạng lạm phát tại Zimbabwe
Trong những tình huống như này, VaR trở thành công cụ đo lường mức độ rủi ro hiệu quả đối với các khoản đầu tư, các tổ chức tài chính (trong khuôn khổ bài viết này là rủi ro của danh mục đầu tư) bởi nó trả lời được 2 câu hỏi quan trọng sau:
Thứ nhất, nếu một sự kiện “thiên nga đen” xảy ra, thiệt hại lớn nhất với danh mục của chúng ta là bao nhiêu?
Thứ hai, xác suất xảy ra trường hợp đó là bao nhiêu (%)?
Để xác định được VaR của danh mục đầu tư (khác với phương sai Var), các bước thực hiện cụ thể như sau:
- Xác định mức phân phối lợi nhuận của danh mục đầu tư
- Lập bảng phân phối để xác định lợi nhuận của danh mục đầu tư có tuân theo Phân phối chuẩn hay không
- Sắp xếp các mốc lợi suất của danh mục đầu tư theo thứ tự giảm dần
- Lựa chọn được 95% tổng số quan sát
- Giá trị nhỏ nhất trong khoảng 95% quan sát chính là VaR của danh mục đầu tư
- Giá trị trung bình của 5% quan sát cuối cùng gọi là CVaR (Cumulative VaR hay CVaR)
Khi đề cập tới VaR, kiến thức nền tảng mà chúng ta cần phải nắm được đó là Phân phối chuẩn (normal distribution) nhằm xác định phân phối các mức lợi suất của danh mục đầu tư. Thật hay là chúng ta đã tính toán xong mức lợi suất chuẩn hóa trong bài viết về “Đường cong vốn chủ sở hữu – Equity Curve”, bạn có thể tham khảo lại các bước thực hiện tại đây.
Sau khi đã tính được mức lợi suất hàng ngày của danh mục đầu tư (1), chúng ta cần xác định được các mức lợi suất này có tuân theo phân phối chuẩn hay không (2). Để làm được điều này, chúng ta cần thực hiện một số bước cơ bản như sau:
Bước 1: Xác định mức lợi suất nhỏ nhất và lớn nhất của danh mục đầu tư trong khoảng thời gian nghiên cứu bằng hàm ‘=Max()’ và ‘=Min()’ trong Excel.

Bước 2 – Xác định số lượng điểm dữ liệu (số quan sát) bằng hàm đếm ‘=count ()’

Sẽ có 126 quan sát về lợi suất trong danh mục ví dụ của chúng ta tương ứng với số ngày giao dịch thực tế của bộ dữ liệu. Một khi đã nắm rõ các bước được thực hiện trong ví dụ này, bạn hoàn toàn có thể áp dụng cho một bộ dữ liệu với nhiều quan sát hơn (lý tưởng nhất là từ 1 năm trở lên) để có một cái nhìn tổng quan và cụ thể nhất về phương pháp này.
Bước 3 – Xác định khoảng giá trị nhất định giữa các mức lợi suất (Bin width)
Bin width được hiểu là một khoảng giá trị nhất định chia dãy giá trị thành các phần bằng nhau.
Trong ví dụ này, Bin width = (Chênh lực giữa mức lợi suất lớn nhất và nhỏ nhất) / số quan sát
= (3.26% – (-2.28%))/126
= 0.24%
Bước 4 – Tạo “bins_array”
Để biểu diễn được các mức lợi suất của danh mục thành dạng biểu đồn phân phối (histogram), cần xác định được 2 yếu tố cơ bản là lợi suất và tần suất xuất hiện của mức lợi suất đó. Do đã tính được chuỗi lợi suất trước đó rồi, trong bước này chúng ta sẽ đi xác định tần suất của chúng.
Theo đó, tần suất cho chúng ta biết số lần một mức lợi suất cụ thể xuất hiện. Chằng hạn như: “danh mục đạt mức lợi suất là 0.5% bao nhiêu lần trong một tháng qua?”. Để xác định được tần xuất, chúng ta sẽ sử dụng hàm “=FREQUENCY” trên Excel, với 2 dữ kiện đầu vào bắt buộc đó là:
- data_array: Một mảng hoặc tham chiếu tới một tập giá trị mà bạn muốn đếm tần suất của nó.
- bins_array: Mảng hoặc tham chiếu tới các khoảng mà bạn muốn nhóm các giá trị trong data_array vào trong đó.
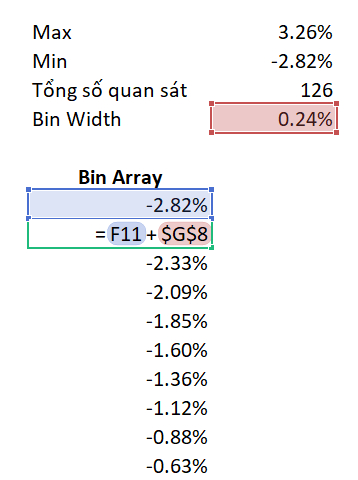
Để xác định được bin_array, chúng ta lần lượt cộng các mức lợi suất trong dãy với giá trị bin width vừa tìm được. Ví dụ:
= -2.82% + 0.24%
= -2.58%
Thực hiện tương tự với toàn bộ mức lợi suất trong chuỗi giá trị, chúng ta có được bảng như sau:
Tiếp theo đó, chúng ta sẽ xác định tần suất xuất hiện của các mức lợi suất điều chỉnh vừa được tính toán xong bằng cách sử dụng hàm ‘=frequency ()’. Kết quả thực hiện như sau:

Hãy luôn ghi nhớ chúng ta đang thực hiện tính toán đồng thời trên các chuỗi dữ liệu, vì vậy để thực hiện hàm tính toán chúng ta cần nhấn tổ hợp phím ‘Ctrl + shift + enter’ thay vì chỉ nhấn ‘Enter’.
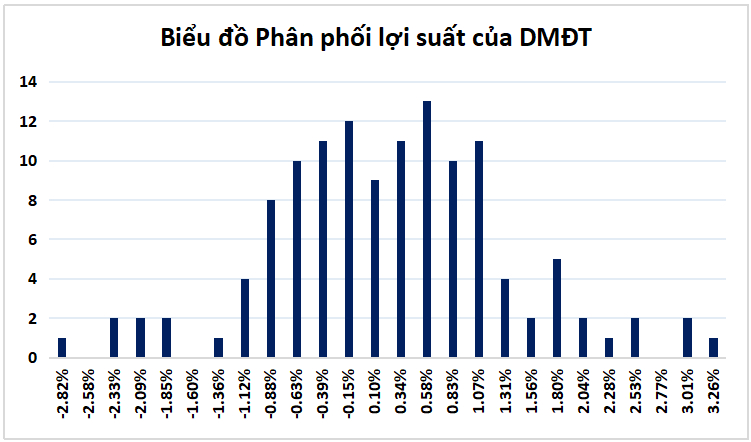
Bước 5 – Lập đồ thị phân phối lợi suất
Thông qua 4 bước đã được thực hiện ở trên, chúng ta đã có dữ liệu về lợi suất và mức tần suất xảy ra tương ứng. Đến bước này, chúng ta chỉ cần vẽ biểu đồ của tần suất để trực quan hóa mức độ phân bố của chúng. Sau khi đã biểu diễn thành 1 biểu đồ, cần quan sát hình ảnh mức độ phân phối có giống với đường cong hình chuông (hình ảnh đặc trưng phân phối chuẩn) hay không.
Kết quả cụ thể như sau:
Giá trị chịu rủi ro – Value at Risk là gì?
Sau khi đã xác định được lợi suất của danh mục tuân theo phép phân phối chuẩn, chúng ta sẽ đi xác định Giá trị chịu rủi ro (VaR) của danh mục. Trước hết cần sắp xếp lại chuỗi dữ liệu về lợi suất theo thứ tự giảm dần.

VaR của danh mục đầu tư được định nghĩa là giá trị nhỏ nhất trong khoảng 95% tổng số quan sát. Chúng ta có tất cả 126 quan sát, như vậy 95% số quan sát sẽ là ~120. Như vậy, với ví dụ của chúng ta, VaR sẽ bằng -1.48%.
Đối với 5% số quan sát còn lại (6 quan sát), giá trị trung bình của nó sẽ tương ứng với VaR tích lũy (CVaR) của danh mục. Như vậy, trong ví dụ của chúng ta, CVaR sẽ = -2.39%.
Một số câu hỏi đặc trưng mà chúng ta thường đặt ra khi tiếp cận với giá trị chịu rủi ro của danh mục đó là:
Tại sao lại cần phải xác định xem lợi suất của danh mục có tuân theo phép phân phối chuẩn hay không?
Khi một bộ dữ liệu tuân theo phân phối chuẩn, điều này đồng nghĩa là 65% số quan sát sẽ nằm xung quanh 1 mức lệch chuẩn (1 SD), 95% dữ liệu sẽ phân bố xung quanh 2 mức lệch chuẩn và 99% dữ liệu sẽ phân bố quanh 3 mức lệch chuẩn.
Như vậy khi một danh mục tuân theo phép phân phối chuẩn, đồng nghĩa với mức lợi suất ngẫu nhiên (vào một ngày bất kỳ) của danh mục sẽ nằm trong khoảng 95% số quan sát này. Và do đó, giá trị nhỏ nhất trong khoảng 95% số quan sát này sẽ phải đại diện cho mức tổn thất (loss) lớn nhất của danh mục đầu tư hay chính là giá trị VaR.
Với giá trị VaR = -1.48%, liệu danh mục có khả năng thiệt hại nhiều hơn nữa không?
Câu trả lời là hoàn toàn có thể xảy ra và đó chính là giá trị CVaR của danh mục. Trong trường hợp đặc biệt, sẽ có khoảng 5% khả năng mức thiệt hại của danh mục vượt qua giá trị VaR (tức -2.39% trong ví dụ trên). Mức thiệt hại của danh mục sẽ hiếm khi vượt qua được giá trị CVaR này nữa.
Hy vọng với những nội dung đã thảo luận ở trên, bạn đã có thể áp dụng ngay chúng với danh mục đầu tư của mình để có một cái nhìn sâu sắc hơn về nó. VaR là một hướng tiếp cận khá thú vị để xác định rủi ro của danh mục và bạn hoàn toàn có thể căn cứ vào nó để cân nhắc điều chỉnh danh mục đầu tư sao cho phù hợp với khẩu vị rủi ro của mình.
Happy trading !